回転体とパップスギュルダンの定理について

このご時世でお仕事が休みになってしまって、暇だからyoutubeでオンライン授業をあさってたら数学の回転体の動画を見つけました。

数学苦手でしたが、回転体について考えてたらパップスギュルダンの定理というものに行きついたのでまとめました。

パップスギュルダンの定理について知りたい方は前置きが長いので下のリンクからどうぞ。

回転体とは？

たしか回転体って、関数を積分して体積を求めるやつですよね？

xが0~1の区間でx軸を中心に回転させる時の式は、

V = ∫¹₀ πy² dx

個人的なイメージですが底面積をある区間でもって積み上げてく感じ。

例えば、

y=1のグラフについて

x=0から1までをx軸を中心に回転させた体積を求めるとすると、

y1

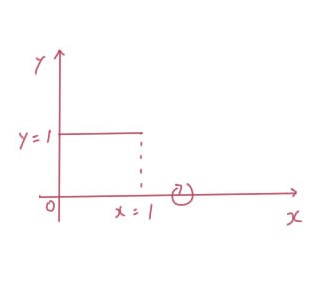
V = ∫¹₀ π 1² dx

   = π [x]¹₀

   = π

要は、

半径=1

高さ=1

の円柱の体積を求めてる感じ。

円柱の体積 = 底面積(半径 × 半径 × π) × 高さ

だから、円柱の体積 = 1 × 1 × π × 1 = π

ですね。

ちょっと気になったのですが・・・

正方形の角を2つ持って、グルっと1周(360度分？それとも円周分？)回しても円柱になるのでは？つまり、360度分か円周分を積分すると体積は求められるのでは？

まず、半径rの円柱の体積は半径r、高さhとすると、

正しい円柱の体積 = r × r × π × h = π = πhr²

1．円周分(2πr)積分する

正方形の縦「r」横「h」とすると面積は「hr」なのでこれを2πr分積分すると

円柱の体積 = ∫^2πr₀ hr dx

みたいなかんじでしょうか？？hrは定数なので、積分すると「hrx」となりますね。

結果は「2πhr²」となりますね。・・・正しい円柱の体積と2倍も違う？？

2．360度分(2π)積分する

同様に2π分積分すると

円柱の体積 = ∫^2π₀ hr dx

結果は「2πhr」となりますね。・・・うーーん？？？

そもそもですが、円の面積ってどう求めてるの？

たとえば長方形の面積を求めるときは、

長方形の面積 = 縦 × 横

「縦の線」が「横の数」だけ積み重なって図形になるって個人的なイメージです。

では円の面積は？

円の面積 = 半径 × 半径 × π

この公式ってどこから来たんでしょう？？

だいぶ前の記憶ですが、小学校の頃に円を何等分かの扇形に切って、それを長方形になるように互い違いに積み重ねて面積を出した記憶があります。

circle

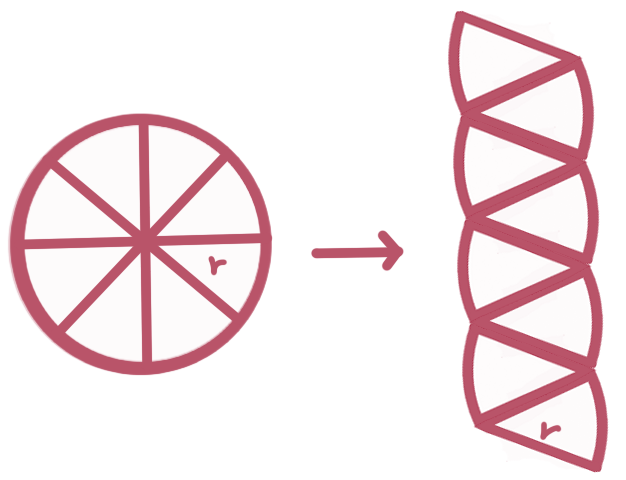
 上の図は8等分にしかしてないので微妙な図形ですが、

短辺が「r」長辺が「円周の半分(πr)」なので

円の面積 = r × πr

半径の値に円周の半分であるπr分を積み重ねるってイメージかな？

まとめ・・・？

以上のことから、円周の半分である 「πr」 分を積算すればよいということがわかりました。

すなわち、

円柱の体積 = ∫^πr₀ hr dx

これで結果が「πhr²」になりました！

では円錐は・・・？

応用を聞かせて円錐の体積も求めてみましょう。まず円錐を求める公式は、

円錐の体積 (V) = 底面積 (πr²) × 高さ(h) × 1/3 = 1/3πhr²

半径が1で高さも1の円錐の体積は「1/3π」になりますね。

・・・1/3っていやな数字。

下図みたいにy=xのグラフで、xが0から1までの区間でx軸を中心にして回転体を求めると円錐になりますね。求めてみると、

V = ∫¹₀ π x² dx

   = π [1/3x³]¹₀

   = 1/3π

数字もあってますね。

y=x

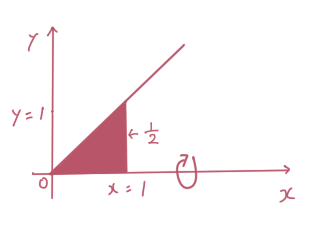
では、さきほど同様に円周の半分を積算してみましょう。

今回は円錐なので、上図の赤く塗りつぶされた部分の「直角三角形」を円周の半分積算します。円周の半分は、「πr」で半径は1なので「π」。

上図の場合の直角三角形の面積は「底辺×高さ÷2」で「1/2」となるので式は、

V = ∫^π₀ 1/2 dx

   =1/2[x]^π₀

   =1/2π

・・・やっぱり。1/3って数字が出てきたときにいやな予感はしてた。

パップスギュルダンの定理について

いくら調べても原因がわからず、いろいろ調べた結果「パップスギュルダンの定理」という定理に行きつきました。

Wikipediaさん曰く、

平面上にある図形 F の面積を S とし、F と同じ平面上にあり F を通らない軸 l の周りで F を一回転させた回転体の体積を V とする。回転させる図形 F の重心 G から回転軸 l までの距離を R としたとき、

V = 2πRS

が成り立つ。この式は、

(回転体の体積 V) = (図形 F の重心 G が回転により描く軌跡の長さ) × (図形 F の面積 S)

と解釈することができる。

まとめ

パップスギュルダンの定理により計算が合わない理由がわかりました。

「円周の半分の積算」でも「360度分の積算」でもなく、

360度(2π) ×「回転軸から図形の重心までの距離」

ですね。

たとえば円柱の場合、パップスギュルダンの定理

V = 2πRS

により図形Fを1×1の正方形だとすると、正方形の重心Rは1/2となりますね。

よって、

V = 2π × 1/2 × 1(正方形の面積) =π

となり正しいですね。

円錐の場合は、

パップスギュルダンの定理

V = 2πRS

により図形Fを底辺1×高さ1の直角三角形とすると、直角三角形の重心は1/3なので、

V = 2π × 1/3 × 1/2(直角三角形の面積) =1/3π

となりますね。

重要なのは

図形 F の重心 G が回転により描く軌跡の長さ

でした。

イメージがわきにくいですが、

ドーナツをイメージして・・・ドーナツを円周方向に垂直にぐるっと1周包丁で細かく切って縦に積み重ねても、外周ほど高くは積みあがらないってことかな。